리지회귀( Ridge regression) vs 라소회귀(Lasso regression) / L1 Norm vs L2 Norm

 

L1 Norm vs L2 Norm

 

L1 Norm

: 빨간색, 파란색, 노란색 경로

: 경로 길이 = 모두 동일한 최단 경로 길이 인 12

: 두 지점 사이를 이동하는 많은 경로가 존재

 

L2 Norm

: 초록색 경로

: 6√2 

: 두 점 사이를 가장 빠르게 가는 한가지 경로 존재

 

 

 

 

리지회귀 Ridge regression, 라소회귀  Lasso regressio

= 선형회귀 + 규제

 

✔️규제

: 모델이 과대적합이 되지 않도록 강제로 제한하기 위해 규제

: 가중치의 절대 값을 가능한 작게 만든다

라소회귀	리지회귀
선형회귀 + L1규제	선형회귀 + L2규제
계수를 0에 가깝게 하려하는데 어떤 계수는 정말 0이 된다 : 모델에서 완전히 제외되는 특성이 생긴다 --> 쉬운 모델	계수를 0에 가깝게 하려 하는데  정말 0이 되는 계수는 없다.

 

여기 중요한 것은 

✔️α✔️ α는 모델을 얼마나 규제할지 조절합니다.

α ↑	α ↓
규제 ↑	규제 ↓
가중치 ↓	가중치 ↑
underfitting (과소적합)	overfitting (과대적합)

 

라소회귀를 보스턴 주택가격 데이터셋을 적용해보면

(기본적으로) α=1 일 때 훈련 세트 점수와 테스트 세트 점수의 결과가 모두 좋지 않습니다.

또한 104개중 4개의 특성만 사용하고 있는데 이는 과소적합이기 때문에 1보다 작은 알파값을 시도해보겠습니다.

 

 

 

α를 0.1,  0.01,  0.001 로 해보니

α를 낮출수록 성능이 좋아지는 것을 알 수 있습니다. 또한 사용되는 특성 수가 점점 늘어납니다. 그만큼 복잡도도 증가한 것입니다. 

하지만 α가 0.001일 때는 너무 α를 낮춰 규제의 효과가 없어 과대적합이 되었습니다.

그래서 α가 0.01일 때 최적입니다.

 

 

 

 

 

 

다시 리지회귀에 보스턴 주택가격 데이터셋을 적용해보면 

(기본적으로) α=1
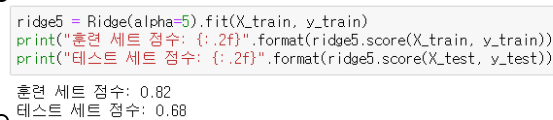
α=5	α=0.1
α=10	α=0.01
α=100

α가 커질수록 성능이 좋지 않은 것을 알 수 있습니다. 따라서 최적의 α를 찾기 위해 α를 작게 할 수록 좋은 성능을 내지만 α를 0.01로 더줄이면 성능이 다시 안좋아집니다. 그러므로 α를 0.1로 설정해줄 수 있습니다.

 

 

 

 

현재 알파가 0.01인 라소모델과 알파가 0.1인 리지모델이 비슷한 성능을 가진다는 것을 알 수 있습니다.

 

하지만 리지모델은 라소모델과 달리 어떤 계수도 0이 아닙니다. 이 두모델 중에서는 보통 리지 회귀를 더 선호합니다. 

 

👉특성의 중요도가 전체적으로 비슷하다면 리지회귀를 선택하는 것이 좋지만

👉많은 특성 중 일부 특성만 중요하거나 분석하기 쉬운 모델을 원한다면 라소회귀가 더 좋은 선택일 수 있습니다.

 

 

 

reference)

www.kaggle.com/residentmario/l1-norms-versus-l2-norms

책 : 파이썬 라이브러리를 활용한 머신러닝